Answers to problems in "Electrode Potentials"

Question 10

The reader is advised to re-read pp. 70-72 before considering this solution.

Cell diagram:

Cd(amalgam, 4.6% Cd) | CdCl2(aq, cM) | AgCl(s) | Ag(s)

Potential determining equilibria:

RHE:

AgCl(s) + e- ⇌ Ag(s) + Cl-(aq)

LHE:

 ½Cd2+ + e- ⇌ ½Cd(amal)

Cell Reaction:

AgCl(s) + ½Cd(amal) ⇌ Ag(s) + ½Cd2+(aq) + Cl-(aq)

The Nernst Equation for this cell reaction is: E = E0cell - {RT/F}ln {aCl- aCd2+½}

(where the activity of cadmium in the amalgam is taken to be unity).

aCl- = f-(2c) and aCd2+ = f+(c). Since c < 10-2M, we can use the DHL. The ionic strength of the solution, I = ½[ 4c +2c] = 3c. Since this is the same for both Cd2+ and Cl-, and since the ratio

zCd2+2/zCl-2 = 4, we can deduce that lg f+/lg f- = 4. ie., f+ = f-4. We can use this result to determine E0cell. However, it is easier and more convenient to use the mean ionic activity coefficient, f±, which is defined on p.48.

f± 3 = f-2 f+ = f-6

Hence, f± = f-2

Hence, aCl- = f±(2c) = f±[Cl-] and aCd2+ = f±(c) = f±[Cd2+]

Therefore, E = E0cell - {RT/F}ln{f±3/2 (2)(c)3/2}

or,

E + {RT/F}ln{2c3/2} = E0cell - {3 RT/ 2F}ln{f±} (*)

or, using DHL, E + {RT/F}ln{2c3/2} = E0cell - {6.909 RT A 31/2 / 2F} c1/2

We plot a graph of E + {RT/F}ln{2c3/2} against c1/2, and extrapolate to find the ordinate intercept (ie. a value for E0cell). The cell emf when aCd2+ = aCl- = 1 corresponds to Ecell.

c / 10-3 mol dm-3 E / V c1/2 / mol1/2 dm-3/2 E + {RT/F}ln{2c3/2} / V

0.1087

0.9023 0.01041 0.56861

0.1269

0.8978 0.01126 0.57007

0.2144

0.8803 0.01464 0.57277

0.3659

0.8641 0.01913 0.57715

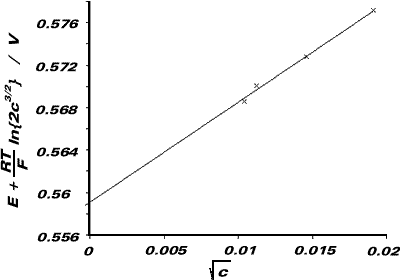
From graph, ordinate-intercept = E0cell = +0.559V

(a). E0cell = E0Ag|AgCl - E0Cd|Cd(amal)

Therefore, E0Cd|Cd(amal) = 0.2222 - 0.559 = -0.3369V

Now consider the cell:

Cd(amal, 4.6% Cd) | CdCl2(aq, 0.5M) | Cd E = -0.0534V

For this cell, E0cell = E0Cd|Cd2+ - E0Cd2+|Cd(amal)

Cell Reaction is:
 Cd2+(aq) + Cd(amal) Cd(s) + Cd2+(aq)

Thus, the Nernst Equation becomes: E = E0cell + {RT/ 2F} ln {aCd2+/ aCd2+}

E = E0cell

Hence, E0Cd|Cd2+ = -0.0534 + (-0.3369) = -0. 39V

Therefore, the S.E.P. for the Cd|Cd2+ couple is -0.39V

This result is consistent with the data supplied in Table 1.1 on p. 21.

(b). The Gibbs free energy of the formation of the hydrated ion Cd2+(aq) refers to the process:

Cd(s) → Cd2+(aq) + 2e-

But this process corresponds to the inverse of the Cd|Cd2+ S.E.P.

Since DG0 = -nFE0, and this process corresponds to a two electron transfer (n = 2),

DG0 = -(2)(96 490)(0.3903)

DG0 = -75.32 kJ mol-1

(c). Using the equation labelled with an asterix (*), we can deduce that the mean ionic activity coefficient (f±) of 0.2144 x 10-3 M CdCl2 is 0.701.