Answers to problems in "Electrode Potentials"
Question 6
The cell diagram is:
| Ag | AgCl | Cl2(g) | Pt |
The cell is reversible in both solid and liquid phases.
| RHE: | ½Cl2(g) + e- ⇌
Cl-(s/l)
|
| LHE: | AgCl(s/l) + e- ⇌ Ag(s/l) + Cl-(s/l) |
Formal Cell Reaction:
| ½Cl2(g) + Ag(s) ⇌ AgCl(s/l) |
We know that G = H - TS and H = U +PV
So, G = U + PV - TS
Therefore, dG = dU + PdV + VdP - TdS - SdT
But, dU = dq + dw (where the bold
derivatives remind us that these two quantities are non-state functions.
[See Price, G, "Thermodynamics of Chemical Processes";
Oxford Chemistry Primer, OUP (in press) for a treatment of state
functions.]
Under reversible conditions, dS = dqrev/T,
and thus, considering only expansion work,
dU = TdS - PdV and so dG = VdP - SdT
Hence, (∂G/∂T)P = -S, or (∂DG/∂T)P = - DS
(where the ∂ refers to a partial derivative. See Sivia, ibid. for more about partial derivatives.)
Since DG = -FE for a one-electron
process,
DS = F(∂E/∂T)P
Therefore, a graph of E against T will enable us to calculate DS.
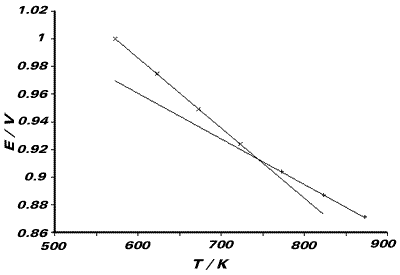
We observe two lines, as the temperature range of
the experiment spans the transition temperature for the AgCl(s)/
AgCl(l) phase change. The melting point of the compound will be
the temperature of the intersection of these two lines. Tfus
= 742.5K One line (viz. the one with steeper gradient)
refers to the cell reaction: ½Cl2(g) + Ag(s) ⇌
AgCl(l). The entropy of this reaction will therefore be related
to the gradient of this line. From the graph, the
gradient is 5.0286 x 10-4V K-1 Similarly,
the other line refers to the cell reaction:
The gradient of this line relates to the entropy
of this cell reaction. From the graph, the gradient is 3.36 x 10-4V
K-1 The entropy corresponding to the phase transition:
AgCl(s) → AgCl(l)
will be the difference of these two entropies.
Hence, since DGfus
= 0 at Tfus (as melting [fusion] is an equilibrium process),
DHfus
= Tfus DSfus
From graph, DSfus = F{5.0286 - 3.36} x 10-4
= +16.1Jmol-1K-1
This is positive as expected, as there is
an increase in molecular randomness (ie. entropy) on going from
the solid to liquid phase.
DHfus
= Tfus DSfus =
+11.95kJmol-1
Reference to a data book (eg. Lide, D R (ed.) "CRC Handbook of Chemistry and Physics", 76th edn., CRC Press, Boca Raton, Florida (1995)) shows that these results are accurate within the limits of experimental error, again illustrating the usefulness of electrode potentials in determining thermodynamic data.


