Answers to problems in "Electrode Potentials"

Question 9

Cell diagram:
Pt | H2 (1 atm) | NH3 (c), NH4Cl (c) | AgCl | Ag

This is (again) a Harned Cell ie.

Pt | H2 | HCl | AgCl |Ag
Potential determining Equilibria:
RHE: AgCl(s) + e- ⇌ Ag(s) + Cl-(aq)

LHE: H+(aq) + e- ⇌ ½H2(g)

Cell Reaction:

AgCl(s) + ½H2(g) ⇌ Ag(s) + H+(aq) + Cl-(aq)

Nernst Equation: Ecell = E0cell - {RT/F}ln{aH+ aCl-},

for PH2 = 1 bar (which approximates to 1 atm., and where E0cell = E0Ag|AgCl (by definition of E0H+|H2 = 0V).

Consider the acid dissociation equilibrium for the ammonium ion:

NH4+(aq) ⇌ NH3(aq) + H+(aq)

The acid dissociation constant for this equilibrium is: Ka = aNH3 aH+ / aNH4+

We notice from the cell diagram that [NH4+] = [NH3] = c.

Thus, Ka = aH+ fNH3 / fNH4+. We can assume that fNH3 = 1. This is very reasonable, because ammonia is an uncharged species. Therefore, Ka = aH+ / fNH4+, which implies that:

aH+ = fNH4+ Ka

Thus, E = 0.2223 - {RT/F}ln{c Ka fNH4+ fCl-}

Now, c < 10-2M, and so the DHL applies. (lg fi = -Azi2 I½) Since zi2 and I are the same for both NH4+ and Cl-,

fNH4+ = fCl- =f± (since HCl is a 1:1 electrolyte) = f

Hence, E + {RT/F}ln(c) - 0.2223 = +4.606RT A I½ / F - {RT/F}ln{Ka}

We now plot a graph of E + {RT/F}ln(c) - 0.2223 against I½ (= c½). This should be a straight line with ordinate-intercept -{RT/F}ln{Ka}.

c / M E / V c / mol dm-3/2 E + {RT/F}ln(c) - 0.2223 / V

0.00857

0.8965 0.09257 0.55198

0.01580

0.8824 0.12570 0.55359

0.02120

0.8757 0.14560 0.55464

0.03030

0.8661 0.18166 0.55620

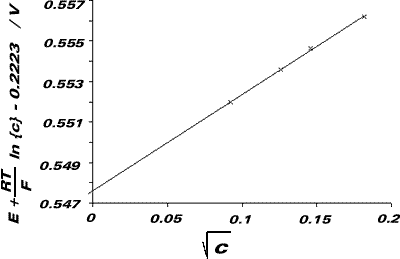
From graph, ordinate-intercept = 5.5 x 10-1V mol-½ dm3/2

Therefore, Ka = 5.5 x 10-10 mol dm-3 (pKa = 9.26)

Kb refers to the forward reaction of the following equilibrium:

NH3 + H2O⇌ NH4+ + OH-

Now, Kw = 1.008 x 10-14 mol2 dm-6 = Ka Kb

Therefore, Kb = 1.008 x 10-14 / 5.5 x 10-10 = 1.7 x 10-5 mol dm-3

Hence, using DG0 = -RT ln Kb, DG0 = +27.2 kJ mol-1

Since DG0 = DH0 - TDS0, DS0 = (4.53 - 27.2) x 10-3 / 298

DS0 = - 76.00 J mol-1 K-1

The protonation of ammonia by water is an entropically disfavoured reaction, a facet manifested in the negative sign of DS0. This is primarily due to the increased ordering of the solvent (water) around the ionic species formed. The unfavourable entropy of solvation combined with the positive (unfavourable) enthalpy of reaction, causes the Gibbs free energy for the (forward) reaction to be positive. Hence, ammonia is only a weak base in water at 298K.