Answers to problems in "Electrode Potentials"
Question 7
The reader is recommended to read pp. 63-66 of the book, to see how to solve this particular problem. Readers looking for innovative and novel ways to solve it are invited to read on!
Harned Cell:
| Pt | H2(g) (P= 1atm) | HCl(aq) | AgCl(s) | Ag(s) |
Potential determining Equilibria
| RHE: | AgCl(s) + e- ⇌
Ag(s) + Cl-(aq)
|
| LHE: | H+(aq) + e- ⇌ ½H2(g) |
Cell Reaction:
| AgCl(s) + ½H2(g) ⇌ Ag(s) + H+(aq) + Cl-(aq) |
Nernst Equation: Ecell = E0cell - {RT/F}ln{aH+ aCl- a Ag / aAgCl PH2 ½}
Notice that since hydrogen is a gas at the temperature of the experiment (298K), we use its partial pressure. ( Strictly, we should talk about the fugacity of hydrogen. This is similar to the concept of activity. However, we can consider hydrogen [to an excellent approximation] as being an ideal gas, with a fugacity coefficient equal to unity.)
Also, since silver and silver chloride are pure solids, their activities can be equated to unity.
Therefore, the Nernst Equation simplifies to: Ecell = E0cell - {RT/F}ln{aH+ aCl-}
Now, aH+ = f+mH+
= f+mHCl, and aCl- =
f-mCl- = f-mHCl
But in the electrolyte solution, the H+ ions and Cl- ions co-exist, and hence, the activity coefficients of the individual ions have no physical meaning. We therefore use the mean ionic activity coefficient f±, which is defined on p.48, for each ionic species.
Therefore, since we are dealing with a 1:1- electrolyte,
f±= (f+ f-)½
Hence, substituting these results into the Nernst Equation, and changing from natural logarthims to decadic logarthims gives:
Ecell = E0cell
- 2.303{RT/F}log mHCl2 - 2.303{RT/F}log {f±2}
| E0cell = E0Ag|AgCl - E0H+|H2 = E0Ag|AgCl | (by definition of E0H+|H2
= 0V) |
Thus, Ecell = E0Ag|AgCl - 2.303{RT/F}log mHCl2 - 2.303{RT/F}log {f±2}
The Debye-Hückel Limiting Law (DHL) states that logf± = -A|z+||z-|I½, where z+, z- are the charges on the ions, A is a temperature and solvent dependent parameter (= 0.509 in water at 298K) and I is the ionic strength of the solution, as defined on p.45. In this case, I = m. [The committed reader will find a derivation of the DHL in chapter 2, Rieger, P H, "Electrochemistry"; Prentice-Hall, New Jersey (1987).]
Hence, we can calculate a value for log f± .
| m / mol kg-1 | I / mol kg-1 | log f± |
|
4 x 10-4 |
4 x 10-4 | -0.01 |
|
9 x 10-4 |
9 x 10-4 | -0.015 |
|
1.6 x 10-3 |
1.6 x 10-3 | -0.02 |
|
2.5 x 10-3 |
2.5 x 10-3 | -0.025 |
We can now determine a value for the Standard Electrode Potential for the silver/silver chloride couple.
Ecell = E0Ag|AgCl
- 2.303(2){RT/F}ln m - 2.303(2){RT/F}log {f±}
or, Ecell + 4.606{RT/F}log {f±} = E0Ag|AgCl - 4.606{RT/F}log m
We now plot a graph of Ecell + 4.606{RT/F}log {f±} against log m. This gives an intercept of EAg|AgCl.
| E / V | I / mol kg-1 | Ecell + 4.606{RT/F}log {f±} | log m |
|
0.62565 |
4 x 10-4 | 0.62447 | -3.398 |
|
0.58460 |
9 x 10-4 | 0.58283 | -3.046 |
|
0.55565 |
1.6 x 10-3 | 0.55329 | -2.796 |
|
0.53312 |
2.5 x 10-3 | 0.53020 | -2.602 |
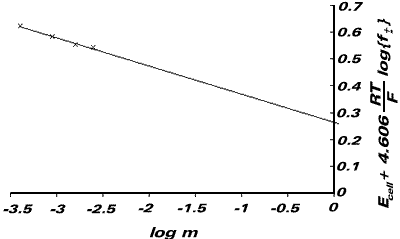
From the graph, E0Ag|AgCl = +0.222V



