Answers to problems in "Electrode Potentials"
QUESTION 12
(i) The half-cell reaction for the anthraquinone monosulphonate redox-couple is
1/2 A(aq) + e- + H+ ⇌ 1/2 AH2 (aq)
which implies the following electrochemical cell
Pt|H2(g) (P=1 atm) | H+(aq) (a=1) ||A(aq)(aA), H+(aq) (aH+), AH2 (aq) (aAH2) |Pt
The corresponding Nernst equation is as follows noting that the hydrogen electrode above is standard
E = E0A/AH2 + RT/F ln[(aA1/2 aH+)/( aAH21/2)]
Since anthraquinone and anthrahydroquinone are neutral molecules and uncharged their activities can, to a good degree of accuracy, by approximated by their concentrations. The Nernst equation is simplified to
E = E0A/AH2 + RT/F ln[ ([A]1/2 aH+)/( [AH2]1/2) ]
(ii) The Nernst equation from (i) can be written as
E = E0A/AH2 + RT/F ln[ ([A]1/2 aH+)/( [AH2]1/2) ] + RF/T ln(aH+)
Substituting log10N = lnN/ln(10) into the above gives
E = E0A/AH2 + RT/F ln[ ([AH2]1/2)/( [A]1/2) ] + ln(10)RF/T log10(aH+)
Noting that pH = -log10(aH+), the Nernst equation can be written in terms of pH
E = E0A/AH2 + RT/F ln[ ([AH2]1/2)/( [A]1/2) ] + ln(10)RF/T pH
Differentiating the above equation with respect to pH gives
dE/d(pH) = -ln(10)RT/F
At 25°C, T = 298K.
dE/d(pH) = -ln(10) x 298 x 8.31 / 96485.3 = -59mV per pH unit
(iii) The generalised redox process
B + ne- + mH+ ⇌ BHm
can be written as an one electron half-cell reaction
1/n B + e- + m/n H+ ⇌ 1/n BHm
The Nernst equation for the generalised redox process is therefore
E = E0B/BHm+ RT/F ln[ (aB1/n aH+m/n)/( aBHm1/n) ]
E = E0B/BHm+ RT/F ln[ (aB1/n)/( aBHm1/n) ] + RF/T ln(aH+m/n)
E = E0B/BHm+ RT/F ln[ (aB1/n)/( aBHm1/n) ] + mRF/nT ln(aH+)
E = E0B/BHm+ RT/F ln[ (aB1/n)/( aBHm1/n) ] + mRF/nT log10(aH+)
Substituting in pH = -log10(aH+) gives
E = E0B/BHm+ RT/F ln[ (aB1/n)/( aBHm1/n) ] + mRF/nT pH
Differentiating the above equation with respect to pH gives
dE/d(pH) = - mRT/nF ln(10)
(iv) Acid dissociation constant, KA, for the dissociation reaction HA⇌ H+ + A- is given by
KA = aH+ aA- / aHA
(v) For A/AH2 system (e.g. anthraquinone/anthrahydroquinone), m = 2, n = 2
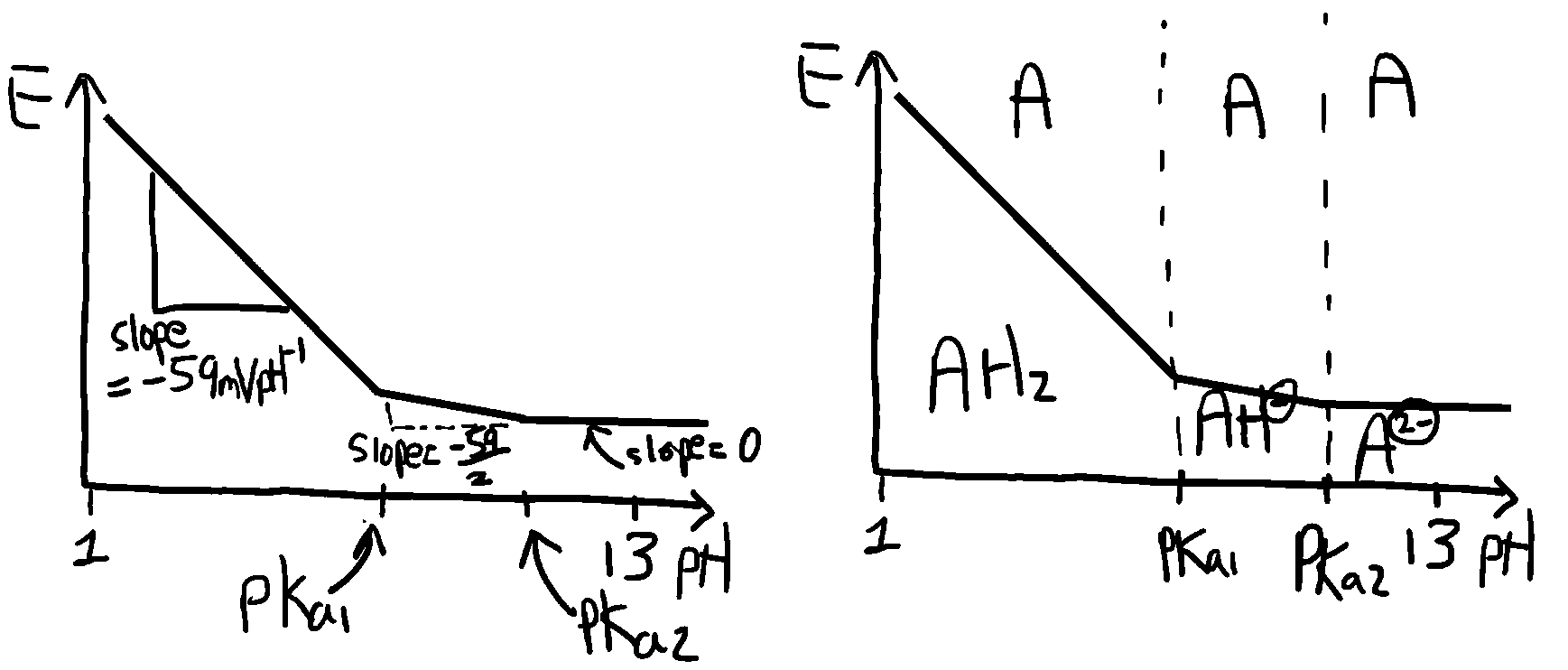
slope = dE/d(pH) = 2RT/2nF ln(10) = -59mV per pH unit
pKa1 (AH-/AH2) = -log(2x10-8)=7.7; pKa2 (A2-/AH-) = -log(1.2x10-11)=10.9
Accordingly, the reduced species (anthrahydroquinone) exists predominantly as AH2 for pH less than 7.7, as AH- in the pH range 7.7 to 10.9 and as A2- for pH > 10.9. Applying the results derived above leads to the following E – pH behaviour using the value n = 2 throughout but m = 0, 1 or 2 as appropriate.
(vi, vii)
|
![]()



