Research
Computational Electrochemistry and Simulation
Any electrochemical problem is a convolution of electrode kinetics and mass transport. Whilst electrode kinetics are well understood, mass transport is more complicated and, in general, must be analysed numerically. In 1905, Cottrell was first solve an electrochemical problem in this way: all calculations being done manually. Widespread use of the technique began in 1964 with Stephen Feldberg's use of a computer to carry out most of the mathematical operations. Subsequent increases in computational speed have allowed more complicated voltammetric experiments to be simulated. The Compton group focuses on the three principal modes of mass transport: diffusion, convection and migration.
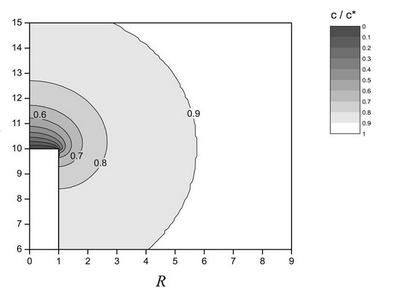
Diffusion is the movement of material across a concentration gradient. It is the most fundamental form of mass transport and is present in all electrochemical experiments. An area of present interest is in the development of numerical techniques for the diffusion of material towards electrodes of novel geometry. Such simulations are relevant to emerging fields including fuel cells and chemical sensors. The figure below shows the concentration profile derived from a cylindrical electrode at steady-state.
Convection is the movement of material either by mechanical means or by density gradients in solution. In the past, several methods have been used to induce convection: most notably rotating disk and channel electrodes. A novel technique uses the electrode to focus a beam of microwaves into solution. Under certain circumstances, the temperature gradient is as high as 105 K cm-1. Such conditions dramatically increase the rate of mass transport towards the electrode and reduce fouling caused by adsorption of unwanted material. Aromatic molecules (such as phenol) are particularly prone to such deposition. The figure shows the limiting current at a microdisc as a function of phenol concentration in both (i) quiescent solution and (ii) microwave irradiated solution. Much higher currents in the latter occur due to the absence of fouling. In collaboration with researchers at the University of Bath, the Compton group is developing numerical methods with which to study this phenomena.
Migration is the movement of charged material due to a potential gradient. A potential gradient can be formed as a result of the electrostatic interaction between an electrode surface and the ions in solution. Despite being of importance to fields as diverse as biology and nanotechnology, migration is poorly understood. In light of this, electrochemists often conduct experiments in the presence of large concentrations of inert salt in order to eliminate potential gradients in solution. The Compton group is developing numerical methods with which to quantify migration in solution.